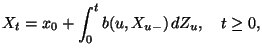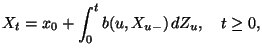15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 12 - Wahrscheinlichkeitstheorie, Statistik
Montag, 17. September 2001, 16.30, Hörsaal 7
Stochastic Equations Driven by Symmetric Stable Processes
Hans-Jürgen Engelbert,
Friedrich-Schiller-Universität Jena
We study stochastic equations
driven by one-dimensional symmetric stable processes 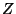 of index
of index 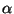 with
with
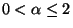 .
Here
.
Here
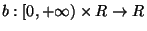 denotes a measurable diffusion coefficient and
denotes a measurable diffusion coefficient and
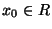 is the initial value.
As special cases for the driving
process
is the initial value.
As special cases for the driving
process 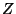 , Brownian motion (
, Brownian motion (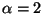 )
and the Cauchy process (
)
and the Cauchy process (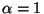 ) are included.
We are interested in general conditions for existence
and uniqueness of weak solutions.
The basic tool is time change of symmetric stable processes.
Using the property that appropriate time changes
of stochastic integrals with respect to
symmetric stable processes are again
symmetric stable processes with the same
index, we present a new approach which completely
unifies the treatment of two quite different cases:
the continuous case (
) are included.
We are interested in general conditions for existence
and uniqueness of weak solutions.
The basic tool is time change of symmetric stable processes.
Using the property that appropriate time changes
of stochastic integrals with respect to
symmetric stable processes are again
symmetric stable processes with the same
index, we present a new approach which completely
unifies the treatment of two quite different cases:
the continuous case (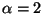 ) and
the purely discontinuous case (
) and
the purely discontinuous case (
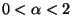 ).
).
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden