15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 5 - Geometrie
Donnerstag, 20. September 2001, 18.00, Hörsaal 50
Überdeckung der Kugel durch kongruente Kreise
Auf der Kugel mit Radius 1 sollen n kongruente Kreise mit Radius 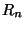 so verteilt werden, daß jeder Kugelpunkt zu (mindestens)
einem Kreis gehört.
Es stellt sich nun die Frage, bei welcher Anordnung von n Punkten der
Überdeckungsradius
so verteilt werden, daß jeder Kugelpunkt zu (mindestens)
einem Kreis gehört.
Es stellt sich nun die Frage, bei welcher Anordnung von n Punkten der
Überdeckungsradius 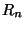 kleinstmöglich wird. Diese Anordnung sei -
soferne sie existiert - die optimale Anordnung für n Punkte.
kleinstmöglich wird. Diese Anordnung sei -
soferne sie existiert - die optimale Anordnung für n Punkte.
Für n = 2-7, 10, 12 und 14 ist diese durch Arbeiten von
L.Fejes-Toth, K.Schütte und G.Fejes-Toth bekannt[1, S. 170f, 209].
Für n = 8 (K.Schütte) und n = 9 (E,Jucovic) sind bereits seit
langem Anordnungen bekannt, die nicht mehr verbessert werden konnten,
deren Optimalität bislang aber noch nicht bewiesen wurde.
Im Vortrag wird nachgewiesen, daß 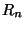 für n = 8 und n = 9
mit den Überdeckungsradien dieser Anordnungen übereinstimmt.
für n = 8 und n = 9
mit den Überdeckungsradien dieser Anordnungen übereinstimmt.
| [1] |
Lazlo Fejes-Toth:
Lagerungen in der Ebene, auf der Kugel und im Raum
Springer, Berlin, zweite Auflage 1972 |
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden