15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 5 - Geometrie
Montag, 17. September 2001, 18.00, Hörsaal 50
Kugelpackungen und Isoperimetrie
Achill Schürmann, Universität Siegen
(Koautoren: Peter Scholl, Jörg M. Wills )
Die Mittelpunkte
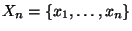 einer endlichen Packung
mit Kugeln vom Radius
einer endlichen Packung
mit Kugeln vom Radius 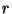 im
im 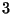 -dimensionalen Euklidischen Raum
definieren ein Packungspolytop
-dimensionalen Euklidischen Raum
definieren ein Packungspolytop
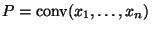 .
Mit einem Satz von FOLKMAN und GRAHAM [1] zeigen wir
.
Mit einem Satz von FOLKMAN und GRAHAM [1] zeigen wir
für die Oberfläche 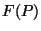 nicht ,,spindelförmiger`` Packungspolytope
nicht ,,spindelförmiger`` Packungspolytope 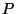 .
Dabei gilt Gleichheit genau dann, wenn sich der Rand
.
Dabei gilt Gleichheit genau dann, wenn sich der Rand
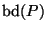 von
von 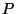 vollständig in reguläre Dreiecke der Kantenlänge
vollständig in reguläre Dreiecke der Kantenlänge 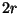 zerlegen läß t,
so daß die Ecken der Dreiecke alle zu
zerlegen läß t,
so daß die Ecken der Dreiecke alle zu 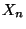 gehören.
Diese oberflächenminimalen Packungspolytope bzw. Kugelpackungen
werden klassifiziert.
Es stellt sich heraus, daß viele von ihnen, z.B. die sogenannten Deltaeder,
Lösungen verschiedener Packungsprobleme sind,
so etwa bezüglich der parametrischen Dichte (vgl. [2]).
Auß erdem ordnen sich die Atome in Microclustern vielfach in dieser Form an.
gehören.
Diese oberflächenminimalen Packungspolytope bzw. Kugelpackungen
werden klassifiziert.
Es stellt sich heraus, daß viele von ihnen, z.B. die sogenannten Deltaeder,
Lösungen verschiedener Packungsprobleme sind,
so etwa bezüglich der parametrischen Dichte (vgl. [2]).
Auß erdem ordnen sich die Atome in Microclustern vielfach in dieser Form an.
| [1] |
J. H. Folkman, R. L. Graham,
A packing inequality for compact convex subsets
of the plane, Canad. Math. Bull.,
12 (1969), 745-752. |
| [2] |
U. Betke, M. Henk and J. M. Wills,
Finite and infinite packings,
J. reine angew. Math., 453 (1994), 165-191. |
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
![]() einer endlichen Packung
mit Kugeln vom Radius
einer endlichen Packung
mit Kugeln vom Radius ![]() im
im ![]() -dimensionalen Euklidischen Raum
definieren ein Packungspolytop
-dimensionalen Euklidischen Raum
definieren ein Packungspolytop
![]() .
Mit einem Satz von FOLKMAN und GRAHAM [1] zeigen wir
.
Mit einem Satz von FOLKMAN und GRAHAM [1] zeigen wir