15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung

16. bis 22. September 2001 in Wien

Sektion 2 - Zahlentheorie
Dienstag, 18. September 2001, 16.00, Hörsaal 41

 

Zur Nichtteilbarkeit von Ordnungen modulo $ u$

Helmut Müller, Universität Hamburg

Im Zusammenhang mit Verallgemeinerung des $ 3n+1$-Problems zeigten FRANCO und POMERANCE in [1] folgendes Resultat

Satz 1. Bezeichnet man mit $ l(u)$ die Ordnung von $ 2$ modulo $ u$ für ungerades $ u$, so besitzt für jede feste Zahl $ q$ die Menge der ungeraden Zahlen $ u$ mit $ q\nmid l(u)$ die asymptotische Dichte 0

Ein erster Versuch, die Aussage von Satz 1 zu quantifizieren, ist in [3] enthalten:

Satz 2. Für jede feste Primzahl $ q\ge3$ gilt für $ x\to\infty$

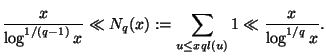
$\displaystyle \frac{x}{\log^{1/(q-1)}x}\ll N_q(x):=\sum_{\substack{u\le x\\ q\nmid l(u)}}1 \ll \frac{x}{\log^{1/q}x}. $

Allerdings wies P. MOREE (vgl. [2]) darauf hin, daß es in der Literatur längst schärfere und auch allgemeinere Ergebnisse in dieser Richtung gibt. Unter Benutzung von Abschätzungen von K. WIERTELAK in [4] konnte er z.B. folgendes zeigen:

Satz 3. Für jede feste Primzahl $ q\ge3$ gibt es eine positive Konstante $ c_q$, so daß für $ x\to\infty$

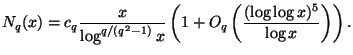
$\displaystyle N_q(x)=c_q \frac{x}{\log^{q/(q^2-1)}x} \left( 1+O_q\left( \frac{(\log\log x)^5}{\log x}\right)\right). $

Bei all diesen Ergebnissen fällt auf, daß ausschließlich die Nichtteilbarkeit der Ordnungen durch primes $ q$ behandelt wird, während doch Satz 1 das Verschwinden zumindest der asymptotischen Dichten bei Nichtteilbarkeit durch beliebige Zahlen $ q$ besagt.

In dem Vortrag soll angedeutet werden, wie man unter Verwendung weitergehender Resultate von K. WIERTELAK zumindest für Primzahlpotenzen $ q=p^n$ analoge quantitative Abschätzungen erhalten kann:


Satz 4. Es seien $ q>2$ prim und $ n\in{\mathbb{N}}$ fest gewählt. Dann gibt es ein $ \alpha'\in]0,1[$, so daß für hinreichend großes $ x$ gilt

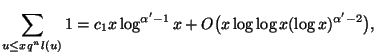
$\displaystyle \sum_{\substack{u\le x\\ q^n\nmid l(u)}} 1=c_1x\log^{\alpha'-1}x+ O\bigl(x\log\log x(\log x)^{\alpha'-2}\bigr), $

wobei $ c_1$ eine positive Konstante ist.

[1] Z. FRANCO, C. POMERANCE, On a Conjecture of Crandall Concerning the $ qx+1$-Problem. Math. Comp. 64, 1333-1336 (1995)
[2] P. MOREE, Improvement of an estimate of H. Müller involving the order of $ 2\pmod u$. Arch. Math. 71, 197-200 (1998)
[3] H. MÜLLER, Eine Bemerkung über die Ordnungen von $ 2\pmod U$ bei ungeradem $ U$. Arch. Math. 69, 217-220 (1997)
[4] K. WIERTELAK, On the density of some sets of primes IV. Acta Arith. 43, 177-190 (1984)

E-Mail: mueller@math.uni-hamburg.de

Zeitplan der Sektion   Tagesübersicht   Liste der Vortragenden