15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 2 - Zahlentheorie
Donnerstag, 20. September 2001, 15.30, Hörsaal 41
On the class number of binary quadratic forms
Manfred Kühleitner, Universität für Bodenkultur,Wien
For each positive integer 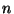 , we
consider the set
, we
consider the set
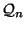 of positive definite, binary quadratic
forms with integral coefficients of discriminant
of positive definite, binary quadratic
forms with integral coefficients of discriminant 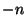 , i.e.,
, i.e.,
Two forms
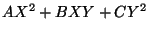 ,
,
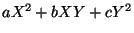 are called equivalent, if
and only if there is a matrix
are called equivalent, if
and only if there is a matrix
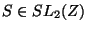 , such that
For a given discriminant
, such that
For a given discriminant 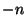 , the number
, the number 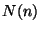 of equivalence classes
is finite. To study the average order of this arithmetic function, we consider
the Dirichlet summatory function
where
of equivalence classes
is finite. To study the average order of this arithmetic function, we consider
the Dirichlet summatory function
where 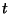 is a large real variable.
In his masterwork Disquisitiones Arithmeticae, C.F. Gauß stated an
approximate formula for
is a large real variable.
In his masterwork Disquisitiones Arithmeticae, C.F. Gauß stated an
approximate formula for 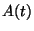 . In this century I. M. Vinogradov
proved several upper bounds for the error term
culminating in
. In this century I. M. Vinogradov
proved several upper bounds for the error term
culminating in
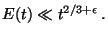 Quite recently, Chamizo and Iwaniec improved this classical upper bound to
where
Quite recently, Chamizo and Iwaniec improved this classical upper bound to
where
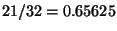 .
The main object of the present paper is to prove a two-sided Omega
estimate for the error term
.
The main object of the present paper is to prove a two-sided Omega
estimate for the error term 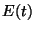 .
.
For real
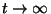 we have
we have
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
![]() , we
consider the set
, we
consider the set
![]() of positive definite, binary quadratic
forms with integral coefficients of discriminant
of positive definite, binary quadratic
forms with integral coefficients of discriminant ![]() , i.e.,
, i.e.,
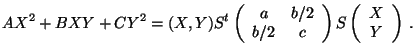
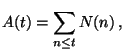
![]() we have
we have