15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 2 - Zahlentheorie
Dienstag, 18. September 2001, 17.30, Hörsaal 41
Über die Anzahl der Untergruppen von endlichen Abelschen Gruppen
Hartmut Menzer, Friedrich-Schiller-Universität Jena
Es sei
hierbei bezeichne 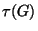 die Anzahl der Untergruppen von einer endlichen
Abelschen Gruppe
die Anzahl der Untergruppen von einer endlichen
Abelschen Gruppe 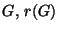 den Rang von
den Rang von 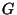 und
und 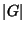 die Ordnung von
die Ordnung von 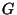 .
Weiterhin sei
.
Weiterhin sei 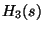 durch die Dirichlet-Reihe
mit der ``level function''
durch die Dirichlet-Reihe
mit der ``level function''
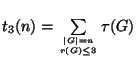 bezüglich
bezüglich 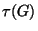 definiert.
definiert.
G. Bhowmik und J. Wu bewiesen im Jahre 1997 für 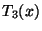 folgende asymptotische
Entwicklung. Es gilt
folgende asymptotische
Entwicklung. Es gilt
(hierbei bedeutet 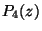 ein Polynom vom Grad 4).
ein Polynom vom Grad 4).
Durch Kombination von drei verschiedenen Resultaten aus der Theorie
höherdimensionaler Exponentialsummen wird für das Restglied 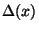 die
verbesserte Abschätzung
die
verbesserte Abschätzung
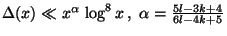 vorgestellt, wenn man für
vorgestellt, wenn man für 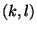 geeignete
Exponentenpaare auf der Basis des Graham-Algorithmus einsetzt. Bereits bei
Verwendung des ``klassischen'' Exponentenpaares
geeignete
Exponentenpaare auf der Basis des Graham-Algorithmus einsetzt. Bereits bei
Verwendung des ``klassischen'' Exponentenpaares
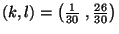 erhält man für
erhält man für
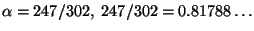 .
.
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
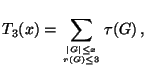
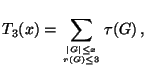
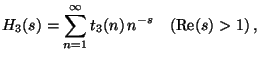
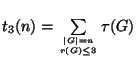 bezüglich
bezüglich ![]() folgende asymptotische
Entwicklung. Es gilt
folgende asymptotische
Entwicklung. Es gilt