15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung

16. bis 22. September 2001 in Wien

Sektion 2 - Zahlentheorie
Montag, 17. September 2001, 16.00, Hörsaal 41

 

Grenzwertsätze in der metrischen diophantischen Approximation

Michael Fuchs, TU Wien

 

Sei $f$ eine positive, monoton gegen 0 fallende Funktion mit der Eigenschaft $\sum_{k=1}^{\infty}f(k)=\infty$. Nach einem klassischen Ergebnis von Khintchine besitzt die diophantische Ungleichung

$$\left\vert x-\frac{p}{q}\right\vert \leq \frac{f(\log q)}{q^2}$$

unendlich viele Lösungen $(p,q),q>0$ für fast alle $x\in [0,1]$.

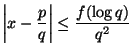
Unter weiteren Voraussetzungen an die Funktion $f$ hat LeVeque in einer Serie von Arbeiten [1] die Anzahl der Lösungen mit $q\leq n$ statistisch untersucht und unter anderem gezeigt, dass ein zentraler Grenzwertsatz gilt, wenn man nur die relativ primen Lösungspaare betrachtet. Ohne diese Einschränkung konnte er keine entsprechende Aussage erzielen. Die Untersuchungen von LeVeque wurden später von Philipp [2] weitergeführt.

In meinem Vortrag behandle ich den Fall aller Lösungen mit $q\leq n$ und zeige Verschärfungen der Ergebnisse von LeVeque und Philipp.

[1]	W.J. LeVeque, On the frequency of small fractional parts in certain real sequences I,II, Trans. Amer. Math. Soc. 87, 1958, 237-260 und Trans. Amer. Math. Soc. 94, 1959, 130-149.
[2]	W. Philipp, Mixing Sequences of Random Variables and Probabilistic Number Theory, Mem. Amer. Math. Soc. 114, 1971, Providence, Rhode Island.

E-Mail:	fuchs@geometrie.tuwien.ac.at
Homepage:	www.geometrie.tuwien.ac.at/fuchs

Zeitplan der Sektion   Tagesübersicht   Liste der Vortragenden