Christoph Baxa, Universität Wien
Christoph Baxa, Universität Wien
Es sei ![]() eine Irrationalzahl mit Kettenbruchentwicklung
eine Irrationalzahl mit Kettenbruchentwicklung
![]() . Ein klassisches Resultat der
Theorie der Gleichverteilung besagt, daß die
Folge
. Ein klassisches Resultat der
Theorie der Gleichverteilung besagt, daß die
Folge
![]() modulo 1 gleichverteilt ist. Zur quantitativen
Untersuchung dieser Tatsache dienen Diskrepanz und
modulo 1 gleichverteilt ist. Zur quantitativen
Untersuchung dieser Tatsache dienen Diskrepanz und ![]() -Diskrepanz,
die mit
-Diskrepanz,
die mit
![]() und
und
![]() bezeichnet werden sollen.
Die Verteilung ist optimal, wenn die beiden (äquivalenten) Bedingungen
bezeichnet werden sollen.
Die Verteilung ist optimal, wenn die beiden (äquivalenten) Bedingungen
![]() und
und
![]() erfüllt sind. Das ist genau dann der Fall, wenn
erfüllt sind. Das ist genau dann der Fall, wenn
![]() eine Zahl beschränkter Dichte ist, d.h.
eine Zahl beschränkter Dichte ist, d.h.
![]() .
Für solche
.
Für solche ![]() betrachtet man die Abbildungen
betrachtet man die Abbildungen
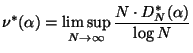 und
und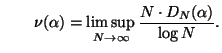
| E-Mail: | baxa@ap.univie.ac.at |
| Homepage: | www.mat.univie.ac.at/~baxa/ |