15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 14 - Partielle Differentialgleichungen, Variationsmethoden
Donnerstag, 20. September 2001, 16.30, Hörsaal 7
Weißes Rauschen in semilinearen elliptischen Differentialgleichungen:der Linearisierungseffekt
Michael Oberguggenberger, Universität Innsbruck
(Koautor: Francesco Russo)
Wir betrachten das Dirichletproblem
Dabei ist
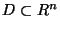 ein beschränktes, glatt berandetes Gebiet,
ein beschränktes, glatt berandetes Gebiet, 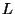 ein
linearer elliptischer Differentialoperator,
ein
linearer elliptischer Differentialoperator, 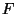 eine beschränkte, Lipschitz-stetige
Funktion,
eine beschränkte, Lipschitz-stetige
Funktion,
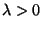 ein Kopplungsfaktor und
ein Kopplungsfaktor und
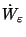 eine durch Faltung geglättete
Version von Gauß schem weiß en Rauschen
eine durch Faltung geglättete
Version von Gauß schem weiß en Rauschen 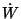 . Für hinreichend kleine
. Für hinreichend kleine 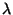 (unabhängig
von
(unabhängig
von
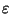 ) gibt es stets eine fast sicher eindeutige Lösung
) gibt es stets eine fast sicher eindeutige Lösung
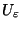 mit glatten
Pfaden. Wir vergleichen diese mit den Lösungen
mit glatten
Pfaden. Wir vergleichen diese mit den Lösungen
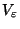 des freien Problems
des freien Problems
welche für
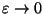 gegen eine verallgemeinerte Lösung
gegen eine verallgemeinerte Lösung 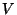 der Gleichung
der Gleichung
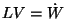 konvergieren. Für
konvergieren. Für 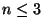 ist dabei
ist dabei 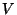 ein Prozess mit stetigen
Pfaden, für
ein Prozess mit stetigen
Pfaden, für 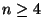 ein verallgemeinerter stochastischer Prozess.
ein verallgemeinerter stochastischer Prozess.
Ziel des Vortrags ist der Nachweis des Linearisierungseffektes: Für eine
groß e Klasse von nichtlinearen Funktionen 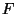 (nämlich aller beschränkten
Funktionen, deren Fouriertransformierte in 0 keine Masse besitzt) konvergiert
im Falle
(nämlich aller beschränkten
Funktionen, deren Fouriertransformierte in 0 keine Masse besitzt) konvergiert
im Falle 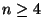 die Differenz
die Differenz
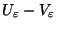 im Quadratmittel gegen Null.
Die Lösungen der nichtlinearen Gleichung verhalten sich also wie jene der
linearen Gleichung. Der Beweis beruht auf einem Lemma der Autoren über Funktionen mit
in Null masseloser Fouriertransformierten und Abschätzungen der Varianz und
Kovarianz der freien Lösung
im Quadratmittel gegen Null.
Die Lösungen der nichtlinearen Gleichung verhalten sich also wie jene der
linearen Gleichung. Der Beweis beruht auf einem Lemma der Autoren über Funktionen mit
in Null masseloser Fouriertransformierten und Abschätzungen der Varianz und
Kovarianz der freien Lösung
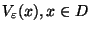 , für
, für
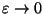 . Der
Linearisierungseffekt wurde auch bei semilinearen hyperbolischen, parabolischen
und Schrödinger-Gleichungen nachgewiesen.
. Der
Linearisierungseffekt wurde auch bei semilinearen hyperbolischen, parabolischen
und Schrödinger-Gleichungen nachgewiesen.
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
![]() (nämlich aller beschränkten
Funktionen, deren Fouriertransformierte in 0 keine Masse besitzt) konvergiert
im Falle
(nämlich aller beschränkten
Funktionen, deren Fouriertransformierte in 0 keine Masse besitzt) konvergiert
im Falle ![]() die Differenz
die Differenz
![]() im Quadratmittel gegen Null.
Die Lösungen der nichtlinearen Gleichung verhalten sich also wie jene der
linearen Gleichung. Der Beweis beruht auf einem Lemma der Autoren über Funktionen mit
in Null masseloser Fouriertransformierten und Abschätzungen der Varianz und
Kovarianz der freien Lösung
im Quadratmittel gegen Null.
Die Lösungen der nichtlinearen Gleichung verhalten sich also wie jene der
linearen Gleichung. Der Beweis beruht auf einem Lemma der Autoren über Funktionen mit
in Null masseloser Fouriertransformierten und Abschätzungen der Varianz und
Kovarianz der freien Lösung
![]() , für
, für
![]() . Der
Linearisierungseffekt wurde auch bei semilinearen hyperbolischen, parabolischen
und Schrödinger-Gleichungen nachgewiesen.
. Der
Linearisierungseffekt wurde auch bei semilinearen hyperbolischen, parabolischen
und Schrödinger-Gleichungen nachgewiesen.