Fritz G. Boese, Max-Planck-Institut für extraterrestrische Physik, Garching
Es werden lineare dynamische Systeme der zeitunabhängigen Ordnung
![]() in diskreter Zeit
in diskreter Zeit
![]() mit skalarem komplexen Zustand
mit skalarem komplexen Zustand
![]() , die für beliebig gegebene komplexe Anfangszustände
, die für beliebig gegebene komplexe Anfangszustände
![]() bis
bis ![]() , durch
, durch
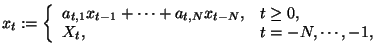 |
(1) |
Es werden hinreichende Stabilitätskriterien für (a) Stabilität
gegen Variation der Anfangszustände und (b) Stabilität im Sinne
von bounded-input bounded-output vorgestellt. Zu den Kriterien
gelangen wir dadurch, daß dem System (1) ![]() -ter Ordnung
(nichttrivial) ein System erster Ordnung mit
-ter Ordnung
(nichttrivial) ein System erster Ordnung mit ![]() -dimensionalen
Zustand in
-dimensionalen
Zustand in ![]() zugeordnet wird. Mit wachsender Ordnung werden
die Kriterien besser.
zugeordnet wird. Mit wachsender Ordnung werden
die Kriterien besser.
Weiters wird eine explizite Lösungsdarstellung für den Zustand
![]() vorgestellt. Resultate von Popenda [1] und Mallik [2]
(und anderen) werden dabei verallgemeinert und einsichtiger gemacht. Auf die
Ergebnisse im multivariaten Fall, also für partielle
Differenzengleichungen, wird eingegangen.
vorgestellt. Resultate von Popenda [1] und Mallik [2]
(und anderen) werden dabei verallgemeinert und einsichtiger gemacht. Auf die
Ergebnisse im multivariaten Fall, also für partielle
Differenzengleichungen, wird eingegangen.
| [1] | J. Popenda, One expression for the solution of a second order linear difference equation with variable coefficients, Proc. Amer. Math. Soc. 100(1987)1, 87-93. |
| [2] | R. K. Mallik, On the solution of a linear difference equations with variable coefficients, SIAM J. Math. Anal. 31(2000)2, 375-385. |
| E-Mail: | gub@mpe.mpg.de |
| Homepage: | www.rosat.mpe-garching.mpg.de/~gub |