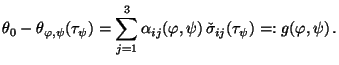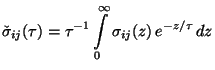15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 10 - Angewandte Mathematik, Industrie- und Finanzmathematik
Montag, 17. September 2001, 16.30, Hörsaal 42
Entwicklung eines Inversionsschemas für die Laplace-Transformation mit einer Anwendung in der Röntgen-Diffraktometrie
Thomas Schuster, Universität des Saarlandes
Bei der Röntgen-Diffraktometrie handelt es sich um eine Form
des zerstörungsfreien Prüfens. Es wird versucht mit Hilfe von
Röntgenstrahlen den Spannungstensor
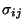 eines Werkstückes
zu rekonstruieren. Unter Beachtung des Hook'schen Gesetzes und der
Bragg'schen Bedingung erhält man folgende Beziehung zwischen der
Differenz der Glanzwinkel der verspannten und der unverspannten Probe
einerseits, und dem Spannungstensor
eines Werkstückes
zu rekonstruieren. Unter Beachtung des Hook'schen Gesetzes und der
Bragg'schen Bedingung erhält man folgende Beziehung zwischen der
Differenz der Glanzwinkel der verspannten und der unverspannten Probe
einerseits, und dem Spannungstensor
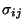 andererseits:
andererseits:
Dabei ist
die reziprok Laplace-Transformierte von
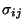 . Die
Rückgewinnung des Spannungstensors aus den Daten
. Die
Rückgewinnung des Spannungstensors aus den Daten 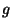 erfordert daher
einen stabilen Inversionsalgorithmus für die Laplace-Transformation.
Dazu wird das Verfahren der approximativen Inversen herangezogen, d.h.
man berechnet statt der gesuchten Objektfunktion
erfordert daher
einen stabilen Inversionsalgorithmus für die Laplace-Transformation.
Dazu wird das Verfahren der approximativen Inversen herangezogen, d.h.
man berechnet statt der gesuchten Objektfunktion 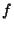 , Momente
, Momente
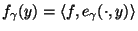 von
von 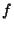 mit
sogenannten Mollifiern
mit
sogenannten Mollifiern 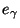 . Liegen diese im Bild des Adjungierten
der Laplace-Transformation
. Liegen diese im Bild des Adjungierten
der Laplace-Transformation 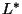 , so reduziert sich die Berechnung
von
, so reduziert sich die Berechnung
von 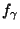 auf die Berechnung von Skalarprodukten der gegebenen
Daten
auf die Berechnung von Skalarprodukten der gegebenen
Daten 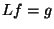 mit sogenannten Rekonstruktionskernen
mit sogenannten Rekonstruktionskernen
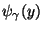 :
wobei
:
wobei
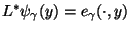 gilt. Im Vortrag wird
zunächst ein Mollifier konstruiert, der an das Bild von
gilt. Im Vortrag wird
zunächst ein Mollifier konstruiert, der an das Bild von 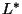 angepaßt ist, anschließend werden die zugehörigen
Rekonstruktionskerne durch ein Kollokationsverfahren bestimmt. An eine
Konvergenzabschätzung für die Kerne schließen sich numerische
Ergebnisse an, die die Wirksamkeit des Verfahrens auch bei gestörten
Daten hervorheben.
angepaßt ist, anschließend werden die zugehörigen
Rekonstruktionskerne durch ein Kollokationsverfahren bestimmt. An eine
Konvergenzabschätzung für die Kerne schließen sich numerische
Ergebnisse an, die die Wirksamkeit des Verfahrens auch bei gestörten
Daten hervorheben.
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
![]() eines Werkstückes
zu rekonstruieren. Unter Beachtung des Hook'schen Gesetzes und der
Bragg'schen Bedingung erhält man folgende Beziehung zwischen der
Differenz der Glanzwinkel der verspannten und der unverspannten Probe
einerseits, und dem Spannungstensor
eines Werkstückes
zu rekonstruieren. Unter Beachtung des Hook'schen Gesetzes und der
Bragg'schen Bedingung erhält man folgende Beziehung zwischen der
Differenz der Glanzwinkel der verspannten und der unverspannten Probe
einerseits, und dem Spannungstensor
![]() andererseits:
andererseits: