15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 10 - Angewandte Mathematik, Industrie- und Finanzmathematik
Dienstag, 18. September 2001, 16.00, Hörsaal 42
Multiskalenanalyse der Eigenschwingungen der Erde
Volker Michel, Universität Kaiserslautern
Eigenschwingungen der Erde werden beispielsweise im Zusammenhang mit schweren
Erdbeben von Seismometern registriert. Sie lassen sich mathematisch mit der
Cauchy-Navier-Gleichung beschreiben. Der Helmholtzsche Zerlegungssatz und die
Miezerlegung erlauben die Unterscheidung von drei Typen von Lösungen, die mit
den Hansenvektoren 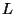 ,
, 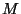 und
und 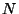 bezeichnet werden. Charakteristisch hierbei
ist, dass
bezeichnet werden. Charakteristisch hierbei
ist, dass 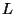 rotationsfrei ist,
rotationsfrei ist, 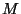 quellfrei und toroidal ist, während
quellfrei und toroidal ist, während 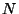 quellfrei und poloidal ist.(Die Begriffe werden im Vortrag näher erläutert.)
quellfrei und poloidal ist.(Die Begriffe werden im Vortrag näher erläutert.)
Ausgehend von dieser Zerlegung kann man mit Hilfe eines Separationsansatzes
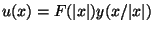 ,
,
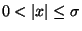 eine (Standard-)Basis von
Fundamentallösungen konstruieren, wobei Besselfunktionen und
Vektorkugelfunktionen Verwendung finden.
eine (Standard-)Basis von
Fundamentallösungen konstruieren, wobei Besselfunktionen und
Vektorkugelfunktionen Verwendung finden.
In dem Vortrag wird zunächst der Zugang zu dieser Basis erläutert. Danach
werden mit Hilfe dieses Funktionensystems Skalierungsfunktionen und Wavelets
konstruiert, die eine Multiresolution für den Raum der Eigenschwingungen der
Erde erzeugen. Die Ausbreitung von seismischen Wellen im allgemeinen ist sehr
komplex und global nur mit groben Modellvereinfachungen beschreibbar. Ein
Multiskalenansatz könnte die Möglichkeit liefern, lokal sowohl Modelle besser
zu integrieren als auch Ergebnisse besser herauszufiltern.
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden