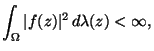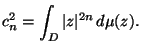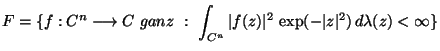15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 8 - Funktionentheorie
Dienstag, 18. September 2001, 16.00, Hörsaal 46
Der kanonische Lösungsoperator für 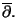
Friedrich Haslinger, Universität Wien
Sei 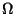 ein beschränktes Gebiet
ein beschränktes Gebiet
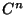 und
und
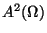 der Bergman Raum aller holomorphen
Funktionen
der Bergman Raum aller holomorphen
Funktionen
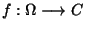 sodass
sodass
wobei 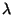 das Lebesgue Maß in
das Lebesgue Maß in
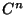 ist.
Wir lösen die
ist.
Wir lösen die
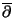 -Gleichung
-Gleichung
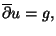 wobei
wobei
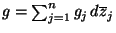 eine
eine
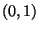 -Form mit Koeffizienten
-Form mit Koeffizienten
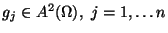 ist mit
ist mit
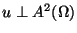 (kanonische Lösung).
Zunächst zeigen wir, dass der kanonische Lösungsoperator für
(kanonische Lösung).
Zunächst zeigen wir, dass der kanonische Lösungsoperator für
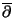 eingeschänkt auf die
eingeschänkt auf die 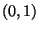 -Formen mit holomorphen Koeffizienten
als Integraloperator mit Hilfe des Bergman Kernes ausgedrückt werden kann.
Dieses Resultat wird dazu verwendet zu zeigen, dass, im Falle des
Einheitskreises in
-Formen mit holomorphen Koeffizienten
als Integraloperator mit Hilfe des Bergman Kernes ausgedrückt werden kann.
Dieses Resultat wird dazu verwendet zu zeigen, dass, im Falle des
Einheitskreises in
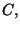 der kanonische Lösungsoperator für
der kanonische Lösungsoperator für
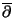 eingeschränkt auf
eingeschränkt auf
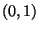 -Formen mit holomorphen Koeffizienten ein Hilbert-Schmidt Operator ist.
Für den Polyzylinder und für die Einheitskugel in
-Formen mit holomorphen Koeffizienten ein Hilbert-Schmidt Operator ist.
Für den Polyzylinder und für die Einheitskugel in
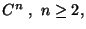 ist der entsprechende Operator nicht mehr
Hilbert-Schmidt.
Wir betrachten auch die Bergman Räume
ist der entsprechende Operator nicht mehr
Hilbert-Schmidt.
Wir betrachten auch die Bergman Räume
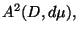 wo
wo
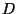 eine Kreisscheibe in
eine Kreisscheibe in
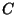 und
und
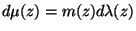 ist, mit einer radialsymmetrischen Gewichtsfunktion
ist, mit einer radialsymmetrischen Gewichtsfunktion 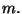 Hier wird noch
vorausgesetzt, dass die Funktionen
Hier wird noch
vorausgesetzt, dass die Funktionen
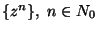 eine orthogonale Basis in
eine orthogonale Basis in
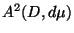 bilden.
Dann erhält man notwendige und hinreichende Bedingungen für
die Kompaktheit und die Hilbert-Schmidt Eigenschaft des kanonischen
Lösungsoperators für
bilden.
Dann erhält man notwendige und hinreichende Bedingungen für
die Kompaktheit und die Hilbert-Schmidt Eigenschaft des kanonischen
Lösungsoperators für
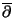 durch Eigenschaften der
Folge
durch Eigenschaften der
Folge 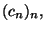 wobei
Schließlich wird auch noch der Fock Raum
behandelt.
wobei
Schließlich wird auch noch der Fock Raum
behandelt.
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
![]() ein beschränktes Gebiet
ein beschränktes Gebiet
![]() und
und
![]() der Bergman Raum aller holomorphen
Funktionen
der Bergman Raum aller holomorphen
Funktionen
![]() sodass
sodass