15. ÖMG-Kongress
Jahrestagung der Deutschen Mathematikervereinigung
16. bis 22. September 2001 in Wien
Sektion 7 - Funktionalanalysis, Harmonische Analysis
Donnerstag, 20. September 2001, 14.00, Hörsaal 28
Arithmetische Mittel des Dirichlet-Kernes
Gilbert Helmberg, Universität Innsbruck
Die Funktion 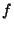 , definiert auf
, definiert auf ![$ [0,\pi]$](helmbergimg2.gif) durch
durch
stellt das arithmetische Mittel des Dirichlet-Kernes 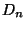 über das
Intervall
über das
Intervall ![$ [0,s]$](helmbergimg7.gif) dar. Obwohl dieser im Intervall
dar. Obwohl dieser im Intervall
![$ ]0,\pi[\;n$](helmbergimg8.gif) Nullstellen
besitzt und seine Schwankung dort die Größenordnung
Nullstellen
besitzt und seine Schwankung dort die Größenordnung 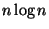 hat,
fällt die Funktion
hat,
fällt die Funktion 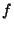 im Intervall
im Intervall ![$ [0,\pi]$](helmbergimg2.gif) monoton von
monoton von 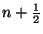 auf
auf 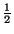 ; sie besitzt dort also genau die Schwankung
; sie besitzt dort also genau die Schwankung 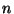 .
.
Die Tatsache, daß das arithmetische Mittel des Dirichlet-Kernes im
Intervall ![$ [0,\pi]$](helmbergimg2.gif) eine Schwankung von der
Größ enordnung
eine Schwankung von der
Größ enordnung 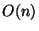 besitzt, ist verantwortlich für eine
Stabilitätseigenschaft des Gibbsschen Phänomens an einer Sprungstelle
einer integrierbaren periodischen Funktion von zwei Variablen.
besitzt, ist verantwortlich für eine
Stabilitätseigenschaft des Gibbsschen Phänomens an einer Sprungstelle
einer integrierbaren periodischen Funktion von zwei Variablen.
| [1] |
Gilbert Helmberg: Localization of a corner-point Gibbs phenomenon for Fourier series in two dimensions. Erscheint im Journal of Fourier Analysis and Applications |
Zeitplan der Sektion
Tagesübersicht
Liste der Vortragenden
![]() , definiert auf
, definiert auf ![]() durch
durch